Position tracking using WiFi signal strength.
We investigate particle filters for state estimation in the context of mobile robotics, people tracking and activity recognition. The animations below illustrate particle filters and their extensions. Just click on the images to get the animations. Have fun!
This animation shows tracking of a person carrying a laptop
measuring wireless signal strengths. The approach uses MCL to track
a person's location on a graph structure, and Gaussian
processes to model the signal strengths of access points.
Position tracking using WiFi signal strength.
See also:
This example shows the ability of particle filters to represent the
ambiguities occurring during global robot localization. The animation
shows a series of sample sets (projected into 2D) generated during
global localization using the robot's ring of 24 sonar sensors. The
samples are shown in red and the sensor readings are plotted in blue.
Notice that the robot is drawn at the estimated position, which is not
the correct one in the beginning of the experiment.
Global localization with sonar.
See also:
In this experiment, we localized the robot globally in a map of the third floor of beautiful Sieg hall, our former Computer Science building. During localization, the sample set size is adapted by choosing the number of samples so that the sample-based approximation does not exceed a pre-specified error bound. The animation shows the sample sets during localization using sonar sensors (upper picture) and laser range-finders (lower picture). At each iteration, the robot is plotted at the position estimated from the most recent sample set. The blue lines indicate the sensor measurements (note the noise in the sonar readings!!). The number of samples is indicated in the lower left corner (we limited the number to 40,000). The time between updates of the animations is proportional to the time needed to update the sample set. In fact, the animations are much slower than the actual processing time (during tracking, a sample set is typically updated in less than 0.05 secs).
The animations illustrate that the approach is able to adjust the number of samples as the robot localizes itself. The number can also increase if the robot gets uncertain. Furthermore, the experiment shows that by simply using a more accurate sensor such as a laser range-finder, the approach automatically chooses less samples.
Global localization with sonar.
Global localization with laser.
See also:
Consider the task of tracking the location of people in an environment that is equipped with ceiling and wall-mounted infrared and ultrasound id sensors, as well as with laser range-finders. The id sensors only provide very coarse location information, while the laser range finders provide accurate location information but do not identify the people. This leads to two coupled data association problems. First, assign anonymous position measurements to the persons being tracked. Second, assign the ids to the persons being tracked based on the id measurements received. We apply Rao-Blackwellised particle filters for this purpose, where each particle describes a history of assignments along with the resulting trajectories of the people. Each particle consists of a bank of Kalman filters, one for each person.
The following animations show results with sensor data recorded at the Intel Research Lab in Seattle. The small blue dots show the end points of the two laser range-finders. The blue dots moving through free space indicate the presence of persons. Note that there are also several false alarms. The filled circles are used to visualize a measurement of an IR-sensor positioned at the center of the circle. The circles have a constant radius of 6.5m, which corresponds to the range up to which the IR-sensors are detecting signals. Ultrasound measurements are visualized using dashed circles, where the radius of the circle corresponds to the distance at which the receiver detected a person. In both cases, the color of the circle indicates the id of the person being detected. The colors of the circles indicate the uncertainty in the person's identity. After a burn in phase, both identities and track associations are sampled.
 Raw data |
 Most likely hypothesis. |
 All hypotheses. |
We developed Rao-Blackwellised particle filters for tracking an object and its interactions with the environment. To do so, the approach estimates the joint posterior over the robot location, the object location, and the object interactions. The video on the left shows the real robot, the animation on the right illustrates the Rao-Blackwellised estimate. Red circles are particles for the robot location, each white circle is a Kalman filter representing the ball's location and velocity. Landmark detections are indicated by colored circles on the field, see also our example of landmark based localization for AIBO robots below.
 Real robot |
 Sample-based belief |
See also:
Consider the task of tracking the location of a person using id sensor data provided by ultrasound and infrared badge systems installed throughout an environment (same as above, but without laser range-finders). Even though particle filters are well suited to represent the highly uncertain beliefs resulting from such noisy and sparse sensor data, they are not the most appropriate representation for this task. We estimate the location of a person by projecting the particles onto a Voronoi graph of the environment (see green lines in right picture). This representation allows more effiicient tracking and the probabilities of the transitions on the graph can be easily learned using EM, thereby adapting the tracking process to a specific user.
 |
 |
See also:
This animation shows three robots as they explore the Allen Center. The robots start from different, unknown locations. Initially, each robot explores on its own and estimates where the other robots are relative to its own map (using a particle filter). Once it finds a good hypothesis for another robot's location, it arranges a meeting with this robot. If the meet, the hypothesis is verified, the robots merge their maps, and coordinate their exploration. Go to our mapping web site for more information.
Distributed exploration from unknown start locations.
See also:
This animation shows Rao-Blackwellised particle filters for map building. The robot trajectories are sampled and, conditioned on each trajectory, a map is built. Shown is the map of the most likely particle only.
SLAM mapping using Rao-Blackwellised particle filters.
See also:
In this project, the particle filter estimates a person's location and mode of transportation (bus, foot, car). A hierarchical dynamic Bayesian network is trained to additionally learn and infer the person's goals and trip segments. The left animation shows a person getting on and off the bus. The color of the particles indicates the current mode of transportation estimate (foot=blue, bus=green, car=red). The middle animation shows the prediction of a person's current goal (black line). Size of blue circles indicates probability of this location being the goal. Right animation shows detection of an error. The person fails to get off the bus at the marked location.
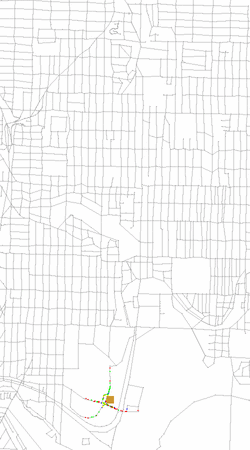 Getting on and off a bus |
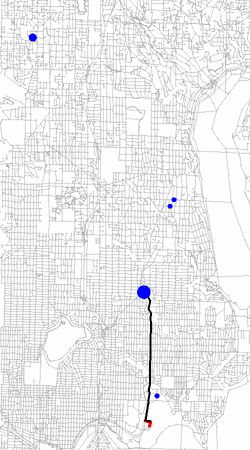 Goal prediction |
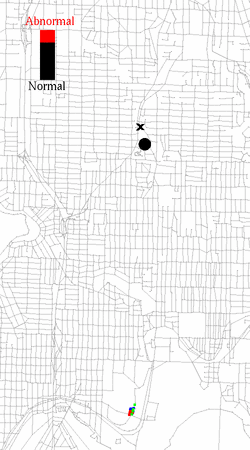 Error detection |
See also:
This animation shows how a Sony AIBO robot localizes itself on a robot soccer field. Landmark detections are indicated by colored circles. To demonstrate re-localization capabilities, the robot is picked up and carried to a different location.
AIBO localization with recovery.
See also:
Due to their sample-based representation, particle filters are less efficient than, e.g., Kalman filters. Therefore, it can happen that the update rate of the sensor is higher than the update rate of the particle filters. Real-time particle filters deal with this problem by representing the belief by mixtures of sample sets, thereby avoiding the loss of sensor data under limited computational resources. The size of the mixture is adapted to the uncertainty using KLD-sampling (see above).
Global localization with laser.
See also:
In this experiment, we apply particle filters to the problem of tracking multiple moving objects. Using its laser range-finders, the robot is able to track a changing number of people even when it is in motion. We address the data association problem by applying joint probabilistic data association filters to particle filters, one for each person.
People tracking with a moving robot.
See also:
This experiment is designed to demonstrate the potential benefits of collaborative multi-robot localization. Our approach makes use of the additional information available when localizing multiple robots by transfering information across different robotic platforms. When one robot detects another, the detection is used to synchronize the individual robots' believes, thereby reducing the uncertainty of both robots during localization. Sample sets are combined using density trees.
The approach was evaluated using our two Pioneer robots Robin and Marian. In this example, Robin performs global localization by moving from left to right in the lower corridor. Marian, the robot in the lab, detects Robin, as it moves through the corridor. As the detection takes place, a new sample set is created, that represents Marian's belief about Robin's position. This sample set is transformed into a density tree which represents the density needed to update Robin's belief. As can be seen in the experiment, the detection event suffices to uniquely determine Robin's position.
Multi-robot localization.
The next animation shows collaborative localization using eight robots (simulated
data).
Multi-robot localization in symmetric environment.
See also:
See also: 
Vision based localization.
F. Dellaert, W. Burgard, D. Fox, and S. Thrun. CVPR-99.